1970 Sampling Variability, Sampling Design and Computation of Standard Errors¹

Estimation

Data summarized from a public use sample not only describe the particular set of households selected in the sample, but are primarily used to estimate what data would have been obtained if a complete census count of the variables of interest were available. Estimates of "true" values (that is, complete counts) may be made from tabulations of public use sample data by using a simple inflation estimate -- that is, by multiplying the sample tally by the reciprocal of the sampling rate. For example, to estimate the total number of persons with a certain population characteristic from a one-in-a-hundred sample, multiply the sample total by 100; i.e., add two zeros to the number tallied from the sample.

Verifying Tabulations

The 1970 public use sample has been constructed so that it should not be difficult to obtain desired tabulations. File structure and coding of items are straightforward. There are no missing data. Records not applicable for each item are tallied in a specific "NA" category and it is not normally necessary to determine in a separate operation whether a record is in the universe or not. A user must, however, anticipate the possibility of errors in his own processing. Thus, user-tabulations should be verified against other available tallies.

Using Control Tabulations from the Samples

As each public use sample was produced, counts of persons, housing units, vacant housing units, and group quarters persons selected into the sample were tallied within each identified geographic area. These control counts will be published as a supplement to this documentation. A failure of user tallies to replicate these exact counts would indicate an error in the user's data processing.

Using Published Data from the 1970 Census

Tabulations from the 1970 census data base are available in the printed census publications and on summary tapes. The tabulations provide an opportunity to check the reasonableness of statistics derived from public use samples. A familiarity with summary data already available may also facilitate planning of tabulations to be made from public use sample data.

In comparing sample tabulations with published data one must carefully note the universe of the published tabulation. For instance, on public use sample records, Industry is reported for the civilian labor force and for persons not in the labor force who reported having worked 1960 or later. Industry tabulations in 1970 census publications are presented only for the employed population or the experienced civilian labor force. Thus, a tally of industry for all persons for which industry is reported on public use sample records would not correspond directly to any published tabulation. One may also wish to note that published reports show "Years of School Completed" while public use samples record "Highest Grade Attended". The highest grade attended must be reduced by one if the respondent is now attending school or did not finish the grade, to yield years of school completed. A user should always pay particular attention to concept. definitions as presented in the Data Dictionary.

One cannot, of course, expect exact agreement between census publications (which are based on the complete census count or on the 20%, 15%, or 5% samples) and user estimates based on tallies of a one-in-a-hundred or smaller sample. They will inevitably differ to some extent due to chance in selection of actual cases for public use samples. Since the amount of likely chance variation for a given statistic can be measured, any discrepancy beyond a certain level can be identified as a likely error in programming. The next section of this chapter discusses sampling variability and its measurement.

User experience has indicated that careful verification of sample tabulations is essential -- so important that it may frequently be advisable to include additional cells in a tabulation for no other reason than to provide counts or to yield marginal totals not otherwise available, which may be verified against other available tabulations.

Sampling Variability

Note: Any user of public use sample data should have a thorough understanding of sampling variability, or should obtain the assistance of a statistician with relevant experience. This discussion should, however, serve as a useful introduction for users with varied backgrounds. Chapter V, "Sample Design and Computation of Standard Errors," includes additional background information.

No one would expect estimates from a one-in-a-hundred sample to be as precise as a complete count of the population. Any number estimated from a sample can differ from its value as derived from a complete count by a factor due to chance; i.e., the chance that one set of persons happened to be selected in the sample instead of another. Symbolically X' = X + e where X' is the estimate derived from a sample, X is the "true" value or census count for a characteristic, and e represents error introduced by chance because a sample rather than the entire population is used in making the estimate. We term this chance variation in an estimate its "sampling variability." If the sampling variability is relatively small, we can be confident that our estimates are fairly accurate and therefore useful. If the sampling variability is relatively large, we have little confidence that we would get anywhere near to the same answer if the sample were drawn over again and we made new estimates. Where chance factors distort the data too much, the estimates may be worthless.

The statistic used to measure sampling variability is the standard error. We will leave a more thorough-going explanation of the standard error and its derivation to the standard statistical texts. Suffice it to say that, for a fixed sample size, the more alike or homogeneous a population is with regard to a particular characteristic the smaller will be the standard error of our estimate of that characteristic; the more heterogeneous, the larger the standard error. The manner in which persons are selected for inclusion in the sample (the sample design) also affects the size of the standard error.

Errors due to chance tend, in the long run, to happen in a particular pattern. About half of them will reduce the estimate and about half of them will increase it. Small errors (errors close to zero) happen more often than large errors. Frequencies or proportions of persons or housing units estimated from a large number of similarly selected samples would tend to cluster in the familiar bell-shaped curve associated with the "normal distribution" for such estimates, the pattern is such that about two-thirds of the time the effect of chance in a sample estimate will be less than its standard error. That is, there is a 68 percent probability that the difference (due to sampling variability) between a sample estimate and a figure obtained by a complete count is less than the standard error. The probability is about 95 percent that the difference is less than twice the standard error, and about 99 percent that it is less than 2-1/2 times the standard error. Stated a different way, once we have derived a sample estimate X' and its standard error (s.e.) we can assume that the chances are about 19 in 20 or 95 percent that the "true" number (X) that we are trying to estimate lies somewhere in the range X' - 2(s.e.) to X' + 2(s.e.).

Example 1. Suppose that we tally a 1-in-100 public use sample for Maryland and find 242 married teenagers aged 14-19 in the sample. Our estimate of the number of married teenagers in the population is then 24,200. If we determine that the standard error of the estimate (i.e., the standard error of the number 24,200) is 1,230 then we conclude that there is a 95 percent chance that a complete census count would be somewhere in the interval 24,200 + (2 x 1,230), or between 21,740 and 26,660. There is still a 5 percent chance that the number of married teenagers is not within that range. If we wanted to be more conservative we could determine instead that there is a 99 percent chance that the complete count of married teenagers in Maryland in 1970 was in the interval 24,200 + (2-1/2 x 1,230) or 21,125 to 27,275. This way we have reduced our chance of making a mistake to one chance in a hundred. As it turns out the 1970 census figure for married teenagers in Maryland is 22,991 which is well inside the 95 percent confidence interval of our estimate of 24,200.

Approximating Standard Errors from Tables A - F

Standard errors are usually estimated using computations from the sample drawn. The processes for doing so are adequately described in the standard statistical texts and, to some extent, in the next chapter. However, since census variables and this method of selecting a sample have already undergone considerable analysis, a shortcut in estimating standard errors for most sample tabulations is possible. Tables A through H provide approximate standard errors for certain types of estimates.

Tables A through F present generalized approximate standard errors computed for the appropriate sample size and size of estimate. The size of the standard error also depends on the nature of the subject variable or characteristic involved and the degree to which that characteristic is affected by the way the sample was selected. The factors in Tables G and H represent this variation: Table G for population subjects, Table H for housing subjects. To determine the standard error for a particular statistic the generalized standard error from one of the tables A through F should be multiplied by the appropriate factor from Table G or H. (The original derivation of Tables A through H is discussed in later in this chapter under a section called "Computation of Standard Errors." There are some limitations to the factors in Tables G and H and these are also discussed.)

Example 2. In Example 1 we cited 1,230 as the approximate standard error of the estimate of married teenagers in Maryland. To obtain this figure we first referred to Table A which provides generalized standard error approximations for 1-in-100 sample data. Since the population of the area we tabulated, Maryland, is just under 4,000,000 we looked for values intermediate between the fourth column (for a population of 1 million) and the fifth column (for a population of 5 million). To determine a generalized standard error for our estimate 24,200 we interpolated between the standard error of 10,000 (s.e. = 990) and the standard error of 25,000 (s.e. between 1,550 and 1,570, or about 1,565), as follows:

s.e.(24,200) = 990 + 24,200 - 10,000 (1565 - 990)
25,000 - 10,000

= 990 + 14200 (575)
15000

= 990 + 544 = 1,534

This provided us with a generalized standard error of about 1,534, but this figure must still be adjusted by a factor representing the relative variability of estimates for marital status and age, as given in Table G. The factor for age is 0. 8 and the factor for marital status is 0.6; the larger factor should be used. Thus the approximate standard error for an estimated 24,200 married teenagers in Maryland can be given by 1,534 multiplied by 0.8. which equals 1,227 or about 1,230.

Tables B, D, and F provide generalized standard errors for percentages or proportions estimated from sample data, the three tables representing 1-in-100, 1-in-1,000 and 1-in-10,000 samples, respectively. Example 3 illustrates their use.

Example 3. Let us say that we are interested in the percent of teenagers in Maryland who are married rather than the actual number of married teenagers. Assuming that we estimate the number of teenagers 14 to 19 years old as 438,200 we estimate the percent of married teenagers to be 24,200 or 5.5 percent.
438,200

The generalized standard error of 5.5 percent when based on an estimated 438,200 cases falls between these values extracted from the table:

estimated
percentage 250,000 500,000

5% 0.44% 0.31%

10% 0.60% 0.42%

By interpolation we may first adjust these figures for the base of the percentage, which is 438,200.

s.e._5% = .44% + 438,200 - 250,000 (.31% - .44%)

500,000 - 250,000

= .44% - .10% = .34%

s.e._10% = .60% +438,200 - 250,000 (.42% - .60%)

500,000 - 250,000

= .60% - .14% = .46%

Then we may interpolate between these two results to get the standard error of 5.5% when based on 438,200.

s.e._5.5% = .34% + 5.5 - 5 (.46% - .34%)

10 - 5

= .34% + .01% = .35%

To obtain the standard error of 5.5 percent as a teenage marriage rate, we must still apply the factor for marital status (0.6) from Table G. (The age variable is present in both the numerator and the denominator of the rate and therefore cancels out.) This gives us .35% x 0.6 = .21%. With roughly 0.2 percent as the standard error of the estimated teenage marriage rate of 5.5 percent we conclude that there is a 95 percent chance that the teenage marriage rate in Maryland is in the range 5.5% + (2 x 0.2%), or between 5.1 percent and 5.9 percent. (According to the census the actual teenage marriage rate is 5.3 percent.)

Applications

Verifying Sample Tabulations. If the difference between the sample estimate and the corresponding statistic found in a census printed report is more than twice the standard error of the estimate, then one should check whether the public use sample estimate was correctly tabulated and the concept definitions were correctly interpreted. Note that even if all tabulations of the public use sample were correctly done, one should expect roughly 5 percent of the tabulated figures to differ from census counts by more than twice the standard error of the public use sample figure.

Determining Confidence Intervals. For a sample estimate we can determine an interval within which the value we are trying to estimate probably lies. The 95 percent confidence interval around an estimate (X') would go from X' - 2(s.e._X') to X' + 2(s.e._X'); i.e., there is only a 5 percent chance that the complete census value is less than or more than that range of values.

Comparing Two Different Areas or Populations. One major use of sample data is to determine whether or not two populations are actually different from one another with regard to a particular characteristic; in other words, whether the estimated difference is large enough that it cannot merely be attributed to chance.

If the difference between the two estimates of the characteristic is more than twice the standard error of that difference then one would normally infer that the two populations actually differ.

The standard error of a difference is estimated by the square root of the sum of the squares of the standard errors of the two statistics; symbolically

s.e._a-b = Ö (s.e._a)² + (s.e._b)²

For example, if we estimated the unemployment rate in Maine as 6.8 percent with a standard error of 0.4 percent and the unemployment rate in New Hampshire as 4.9 percent with a standard error of 0.5 percent then the standard error of the difference would be:

______________ ________________
s.e._D = Ö (.004)² + (.005)²= Ö .000016 + .000025

_______
= Ö .000041 = .0064 or .64%

The difference in, unemployment rates between the two States is 6.8% - 4.9% = 1.9% which is about three times the estimated standard error of the difference. Thus we can conclude that there is better than a 99 percent chance that a complete count of the employment characteristics of the populations in the two States would confirm that the unemployment rate is higher in Maine than in New Hampshire.

This same technique may also be used to measure the reliability of differences in a population as estimated from the 1960 public use sample and a 1970 public use sample.

Comparing Public-Use Sample Data with Published Sample Data. When comparing 1970 public use sample data with published 25 percent sample data from the 1960 or 1950 census, the above formula for the standard error of a difference is directly applicable. The standard error of the published figure may be derived from tables which appear in the same published report.

When comparing 1970 public use sample data with published 1970 sample data the above formula does not apply. Since the public use samples are subsamples of the 15 percent or 5 percent samples, data from the two sources would be correlated. Sampling variability of a difference is consequently reduced. The standard error of a difference between a sample estimate and a subsample estimate (s.e._ss-s) is given by the square root of the difference of the squares of the two corresponding standard errors; symbolically:

________________
s.e._ss-s = Ö (s.e._ss)² - (s.e._s)² .

The standard error of a published sample statistic (s.e._s) is derived from tables in sample data publications.

A user may wish to use this more complicated approach when. verifying public use sample tabulations against census sample tabulations. The earlier discussion of verifying tabulations refers only to the standard error of the public use sample estimate, which alone will be slightly larger than the standard error of the difference (s-e._{ss_s}), and thus will be a slightly less sensitive instrument for detecting tabulation errors than s.e._ss-s .

Determining What Sample Size is Necessary. Larger samples are used only to increase the reliability or precision of sample estimates. Tables A through H allow us to approximate the precision of a sample estimate for alternative sample sizes. For example, we may wish to measure the frequency of a particular characteristic and guess beforehand that it is about 10 percent. We might determine from the tables that a 1/100 sample would yield a standard error of 0.2 percent whereas a 1-in-1000 sample would yield a standard error 0.7 percent. If, for our purposes, we determine that a 95 percent confidence interval of +1.4 percent would be satisfactory, then we may choose to work with only the 1-in-1000 sample.

Sampling Variability of Medians

The sampling variability of a median depends on the number of sample cases and on the distribution on which the median is based. An approximate method for measuring the reliability of an estimated median is to determine an interval about the estimated median such that there is a stated degree of confidence that the true median lies within the interval. As the first step in estimating the upper and lower limits of the interval (that is, the confidence limits) about the median, compute one-half the number of sample cases in the distribution (designated N/2). Look up or compute the standard error of N/2; subtract this standard error from N/2. Cumulate the frequencies (in the table on which the median is based) up to the category containing the difference between N/2 and its standard error, and by linear interpolation obtain a value corresponding to this number. In a corresponding manner, add the standard error to N/2, cumulate the frequencies in the table, and obtain a value corresponding to the sum of N/2 and its standard error. The chances are two out of three that the median would lie between these two values. The range for 19 chances out of 20 and for 99 in 100 can be computed in a similar manner by multiplying the standard error by the appropriate factors before subtracting and adding to N/2.

Sampling Variability of Estimated Means

The sampling variability of a mean, such as the number of children ever born per 1,000 women, depends on the variability of the distribution on which the mean is based., the size of the sample, the sample design and the estimation scheme used. An approximation to the variability of the mean may be obtained as follows: compute the standard deviation of the distribution on which the mean is based; then multiply this figure by a factor from Table G or H appropriate for the particular subject. Divide this product by the square root of the number of sample cases in the distribution.

Estimating Standard Errors for Other Derived Figures

The standard error tables A through H are primarily applicable to estimates of levels (frequencies) or percentages. Estimates of those same standard errors could also have been derived by using computations made directly from the sample data. This is not necessarily warranted since the standard error of an estimate computed from the sample is itself an estimate subject to sampling variability and since such computation is rather cumbersome and costly.

On the other hand, it is not possible to use the tables in measuring the sampling variability of indexes, correlation coefficients, regression coefficients, means and other derived figures. To obtain estimates of standard errors for these derived figures will require extra work. One method is to make computations of the statistic of interest for random subgroups of the sample., and then examine the variability among the estimates produced by the various subgroups. Procedures for estimating standard errors in this way are discussed in the next chapter.

Nonsampling Errors

Sampling error is only one of the components of the total error of a survey. Further contributions may come, for example, from errors introduced by imputations for non-reporting and from errors introduced in the coding and other processing of the questionnaires. These nonsampling errors would usually have also affected a complete census. Standard errors, as discussed in previous sections, measure the precision of a sample estimate relative to a census count. They do not reflect any potential inaccuracy in a census.

For estimates of totals representing relatively small proportions of the population., the major component of the total survey error tends to be the sampling error. As the estimated totals approach the level of the total population., the sampling errors decrease. This is not necessarily true of the nonsampling errors and they assume a relatively larger role in the total survey error. For this reason., the presence of nonsampling errors should be recognized in increasingly larger proportions for estimates close to the total population of an area.

Allocations

Any large collection of data inevitably suffers to some extent from missing data in its basic records resulting. from incomplete questionnaires, inconsistent information (e.g., a two-year-old listed as the head of household), or simply a malfunction in converting the data into machine-readable form. All 1970 census returns were edited to identify inconsistencies and nonresponses, usually resulting in the imputation of likely values. Where possible, unknown or inconsistent information for a person was allocated based on known characteristics. The allocation in many cases was obvious and straightforward, such as the imputation of a missing marital status for a person identified as the wife of the head. In other cases the value allocated was derived from that of a nearby person with similar characteristics; for example, allocations for missing incomes were drawn from the record of the last person processed with the same sex, race, and household relationship, and similar age and employment characteristics. On the other hand, for some items, such as place of birth or occupation, allocation was not appropriate and a "not reported" category appears in the record. It was sometimes necessary, due to nonresponse or to a mechanical difficulty in processing the data, to impute characteristics for persons or households for whom almost no information was available. In this case the record of a nearby person or household was duplicated and substituted for the missing record.

The overall impact of the editing performed on 1970 census data was somewhat greater than in the 1960 census. More sophisticated and detailed procedures were used to detect more types of possible inconsistencies within the records. The allocation rates for the various subjects in the full census samples are presented in the printed reports.

Sample Design

Selection of the 15 Percent and 5 Percent Samples

For sample data collected in the 1970 census, the housing unit, including all its occupants, was the sampling unit; for persons in group quarters identified in advance of the census, it was the person. In non-mail areas (areas in which the respondent was not asked to return his questionnaire by mail), the enumerator canvassed his assigned area and listed all housing units in an address register sequentially in the order in which he first visited the units, whether or not he completed the interview. Every fifth line of the address register was designated as a sample line, and the housing units listed on these lines were included in the sample. Each enumerator was given a random line on which he was to start listing and the order of canvassing was indicated in advance, although the instructions allowed some latitude in the order of visiting addresses. In mail areas, the list of housing units was prepared prior to Census Day either by employing commercial mailing lists corrected through the cooperation of the post office or by listing the units in a process similar to that used in non-mail areas. As in non-mail areas, every fifth housing unit on these lists was designed to be in the sample. In group quarters, all persons were listed and every fifth person was selected for the sample; information on the housing characteristics of group quarters was not collected in the census.

This 20 percent sample was subdivided into a 15 percent and a 5 percent sample by designating every fourth 20 percent sample unit as a member of the 5 percent sample. The remaining sample units became the 15 percent sample. Two types of sample questionnaires were used, one for the 5 percent and one for the 15 percent sample units. Some questions were included on both the 5 percent and 15 percent sample forms and therefore appear for a sample of 20 percent of the units in the census. Other items appeared on either the 15 percent or the 5 percent questionnaires.

Although the sampling procedure did not automatically insure an exact 20 percent sample of persons or housing units in each locality, the sample design was unbiased if carried through according to instructions; generally for larger areas the deviation from 20 percent was found to be quite small. Biases may have arisen, however, when the enumerator failed to follow his listing and sampling instructions exactly. Quality control procedures were used throughout the census process, however, and where there was clear evidence that the sampling procedures were not properly followed, some enumerators' assignments were returned to the field for resampling. Estimates for the United States as a whole indicate that 19.6 percent of the total population and 19.7 percent of the total housing units were enumerated on sample questionnaires.

The computation of these proportions excluded several classes of the population and housing units for which no attempt at sampling was made. These were the relatively small numbers of persons and housing units (in most States, less than one percent) added to the enumeration from the post-census post office check, the various supplemental forms, and the special check of vacant units. However, the ratio estimation procedure described below adjusts the sample data to reflect these classes of population and housing units.

Ratio Estimation Procedure for Published Sample Data

The statistics based on 1970 census sample data are estimates made through the use of ratio estimation procedures which were applied separately for the 5-, 15-, and 20 percent samples. The first step in carrying through the ratio estimates was to establish the areas within which separate ratios were to be prepared. These are referred to as "weighting areas". For the 15- and 20 percent samples, the weighting areas contained a minimum population size of 2,500. The weighting areas used for the 5 percent ratio estimate were larger areas having a minimum population size of 25,000 and comprising combinations of the weighting areas used for the 15- and 20 percent samples. Weighting areas were established by a mechanical operation on the computer and were defined to conform, as nearly as possible, to areas for which tabulations are produced.

The ratio estimation process for population data operated in three stages. The first stage employed 19 household-type groups (the first of which was empty by definition); the second stage used two groups: head of household and not head of household; and the third stage used 24 age-sex-race groups. The groups at each stage are outlined on page below.

At each stage, for each of the groups, the ratio of the complete count to the weighted sample count of the population in the group was computed and applied to the weight of each sample person in the group. This operation was performed for each of the 19 groups in the first stage, then for the two groups in the second stage and finally for the 24 groups in the third stage As a rule, the weighted sample counts within each of the 24 groups in the third stage should agree with the complete counts for the weighting areas. Close, although not exact, consistency could be expected for the two groups in the second stage and the 19 groups in the first stage.

In order to increase the reliability, a separate ratio was not computed in a group whenever certain criteria pertaining to the complete count of persons and the magnitude of the weight were not met. For example, for the 20 percent sample the complete count of persons in a group had to exceed 85 persons and the ratio of the complete count to the unweighted sample count could not exceed 20. Where these criteria were not met, groups were combined in a specific order until the conditions were met.

Each sample person was assigned an integral weight to avoid the complications involved in rounding in the final tables. If, for example, the final weight for a group was 5.2, one-fifth of the persons in the group (selected at random) were assigned a weight of 6 and the remaining four-fifths a weight of 5.

Group:

STAGE I

Male head with own children under 18
1	1-person household
2	2-person household
3	3-person household
.	.
6	6-or-more-person household
Male head without own children under 18
7-12	1-person to 6-or-more-person households
Female head
13-18	1-person to 6-or-more-person households
19	Group quarters persons

STAGE II

20	Head of household
21	Not head of household (including persons in group quarters)

STAGE III

Male Negro
22	Age under 5 years
23	5-13
24	14-24
25	25-44
26	45-64
27	65 and older
Male, not Negro
28-33	Same age groups as for Male Negro
Female Negro
34-39	Same age groups as for Male Negro
Female, not Negro
40-45	Same age groups as for Male Negro

An analogous procedure of ratio estimation was carried out to assign weights for each housing unit for use in preparing census publications of housing data. Weights assigned to housing units were not used in selection of households for public use samples, but were used in the selection of vacant units for the samples. The three groups -- year-round vacant for sale, year-round vacant for rent, and other vacant -- were separately ratio estimated.

The ratio estimates realize some of the gains in sampling efficiency that would have resulted had the population been stratified into the groups before sampling. The net effect is a reduction in both the sampling error and possible bias of most statistics below what would be obtained by weighting the results of the sample by a uniform factor (e.g., by weighting the 20 percent sample by a uniform factor of 5). The reduction in sampling error will be trivial for some items and substantial for others. A by-product of this estimation procedure is that estimates for this sample are, in general, consistent with the complete count for the population and housing unit groups used in the estimation procedure.

Selection of One-in-a-Hundred Samples

Each of the three 1-in-100 samples drawn from 15 percent sample records was created using a systematic selection of, effectively, one-in-fifteen within each of 75 strata. At the same time, three 1-in-100 samples were drawn from 5 percent sample records using a systematic selection of, effectively, one-in-five within the same strata for each sample. The strata were defined in terms of 1970 census data and, with only minor exceptions, employ the characteristics used to establish the ratio-estimation cells derived in preparing the weights carried on the 5 percent and 15 percent sample records. The selection method was designed to sample cases from each geographic area and stratum in proportion to its frequency in the population. It may be considered a valid proportionate sample for all types of areas or subunits of the population.

The designation of the six 1-in-100 (or 1 percent) samples is illustrated by the selection of one of the 1 percent samples from the 15 percent sample census records. To designate the sample, a set of counters -- one for each of the strata -- is reserved. Each counter is assigned an initial value or random start number, between 0 and 99.

Each sample unit -- household, group quarters (GQ) person, or vacant housing unit -- in the original data file is considered in turn. The computer examines the data given on the record and classifies the unit into the proper stratum. The 15 percent sample weight of the unit is added to the existing value in the counter for that stratum. If the unit involved is an occupied unit, the weight assigned to the household head is used for cumulation; if it is a GQ person or a vacant housing unit, the weight for the GQ person or for the vacant housing unit is cumulated.

A sample unit is selected for the 1 percent sample if the addition of its weight causes the cumulation of weights for the stratum to equal or pass a multiple of 100. When an occupied housing unit is selected, each member of the household, as well as the housing unit itself, becomes part of the public use sample.

Three one-in-a-hundred samples were actually drawn from 15% sample records. Thus three sets of counters were used, one for each sample. For the second sample the random start numbers were incremented by 33 and for the third sample, by 66. The 15 percent weight of each 15 percent sample unit was cumulated in the appropriate stratum for each of the three samples. When the cumulation passed a multiple of 100 in one of the sets of counters that sample unit became part of the associated 1 percent sample. Since no 15 percent weight ever was as large as 34 it was impossible for a single sample unit to be selected into more than one of the 1 percent samples, and thus the samples are mutually exclusive.

The three one-in-a-hundred samples drawn from 5 percent data were selected in exactly the same manner using the 5 percent weights assigned to the sample units. For practical purposes, these three 1 percent samples may also be considered mutually exclusive since the probability that a given case will appear in more than one public use sample is less than .001.

Selection of the One-in-a-Thousand and One-in-Ten-Thousand Subsamples

As each sample unit was selected for inclusion in a 1-in-100 sample it was assigned a "subsample number" between 00 and 99. Units were numbered independently within the 75 strata. The first unit selected within a particular stratum was assigned 00, the second 01, the third 02, and so on through 99 and beginning again with 00 for the 101st case selected within the stratum. Thus within a 1 percent sample any two-digit subsample number would identify a systematic selection of roughly 1/100 of the sample cases within each stratum; over all strata, this would constitute a proportionate stratified subsample of the one-in-a-hundred sample, representing one-in-ten- thousand of the total population.

A one-in-ten-thousand sample was extracted from each of the six 1-in-100 samples and is available as a single tape file. Each contains all records assigned the subsample number 60. A one-in-a-thousand sample was also extracted from each 1-in-100 sample using cases with subsample numbers ending in zero (i.e., 00, 10, 20 .... 90). The 1-in-10.,000 samples are thus also subsamples of the extracted 1-in-1,000 subsamples.

User Selection of Samples of Intermediate Size

Samples of any size between 1/100 and 1/10,000 may be selected by using appropriate combination of the 100 1-in-10,000 samples. A 1-in-2,000 sample could be selected from a 1-in-100 sample by choosing sample cases with subsample numbers 00, 20, 40, 60, and 80, (or any other 5 numbers -- though clustering the numbers like 00, 01, 02, 03, and 04 might slightly increase standard errors).

Computation of Standard Errors

The topic of sampling variability is discussed in the first half of this chapter with reference to approximate standard errors derivable from tables A through G. The discussion that follows deals with the derivation of the figures in tables A through G and their limitations, and with the computation of standard errors from the public use samples themselves.

Derivation of Approximate Standard Errors for Tables A through F and G through H

The standard error of an estimate depends on sample size, method of sampling, and the estimation process. If the estimates were made from a completely random sample then the following formula for the standard error of a proportion applies:

where f is the fraction of all units in the sample (e.g., .01, .001, or .0001), p is the estimated proportion, and nis the number of sample units on which the proportion is based. The standard error of an estimated number X' when estimated from a population of size N would simply be equal to the standard error of the proportion (X'/N), multiplied by N. Standard errors for tables A through F were derived by applying these formulas. These tables cannot, however, be directly applied to estimates from these samples since public use samples are not purely random samples but are affected by clustering and stratification in the selection processes. Hence the necessity of applying factors from Tables G and H.

In a cluster sample, as was used for population items (clustering was by household and the persons in each household comprised the cluster), the standard errors may vary from one statistic to another, depending on the homogeneity of the item within a cluster. For instance, the characteristic "mother tongue" is very much clustered by household; people within a single household will almost always have the same mother tongue. Homogeneity within clusters tends to increase the sampling variability, and thus a factor must be applied to adjust "theoretical" standard errors as presented in Tables A through F. The factor for tabulations of person by mother tongue is given as 1.5 in Table G. Since the characteristic "age" for all of the persons in a household is much more varied and less homogeneous, the factor in Table G for age is much less than the factor for mother tongue.

Note that factors for housing items in Table H are always 1.0 or less. Since there was no clustering in the selection of housing units, standard errors are not increased by homogeneity within clusters when tabulating households or housing units. Of course if persons were being tallied with reference to a housing item, e.g., person living in housing units without complete plumbing, then high homogeneity within clusters would exist, and a factor around 1.7 would be appropriate.

Sampling variability for public use samples is reduced by the stratification used in the selection process compared to what would have been obtained by a simple random sample. For instance, we controlled the proportion of vacant units very closely to that obtained in the census, and thus we have improved on the standard error that would have been obtained from a random sample used to estimate the number of vacant units. Thus some factors are less than 1. Factors in Tables G and H show the net affect of increased sampling variability due to clustering (Table G only) and the decreased variability due to stratified systematic sampling.

The stratification in public use sample selection actually took place in two processes: first, the ratio estimation process used in assigning weights to units in the source file accomplished some of the benefits of stratification; secondly, 75 strata were used in the selection of the actual cases for public use samples. The factors in Tables G and H do not account for the benefits of the second process. The factors in Tables G and H are based on computations from the weighted full-census samples. The factors constitute the best approximations available at the time of publication, and should be quite satisfactory for most purposes. More precise estimates of standard errors could be determined empirically from the samples.

A different approach to approximating standard errors based on some empirical work with a 1-in-1,000 sample from the 1960 census and are discussed in the previous chapter on 1960 Sample Design and Sampling Variability.

Standard Errors for Intermediate Size Samples

Tables A through F provided for the one-in-one- hundred, one-in-one-thousand, and one-in-ten- thousand samples may also be used to approximate the errors for intermediate-sized samples by adjusting for sample size. One may note that, for a given size of estimate and a given size of the base population, the standard error from a 1-in-1000 sample is about 3.1 times larger than the standard error of the same estimate derived from a 1-in-100 sample. The 3.1 is really the square root of the ratio of the two sampling rates, as in the following example.²

formula image

It is possible to similarly determine the standard error for a user-selected sample of intermediate size. For instance for a three-in-one-thousand sample a standard error could be determined by looking up the standard error of the same estimate based on a one-in-one- thousand sample (Table B) and multiplying it by

or about 0.58.

The principle is also applicable when combining public use samples to achieve a sample size larger than one-in-a-hundred. If, for instance, two one-in-a- hundred samples,-one of 5 percent data and the other of 15 percent data, are combined for the same area to get estimates of items common to both, the standard errors could be derived by determining those for a 1-in-100 sample, and multiplying each by

or about .707.

The use of such a larger sample size reduces the standard error by almost 3/10.

Estimation of Standard Error for Types of Statistics Not Shown in the Tables

Standard errors are usually not computed for every possible statistic of interest produced in a survey because the estimated standard error is a sample statistic also subject to sampling variability.

Tables A through H apply only to estimated frequencies or proportions and can be adapted for medians. Where other statistics such as means, ratios, indexes, or correlation coefficients are being estimated, the standard error of that figure must be estimated by making computations from the sample itself. This is possible by means of the random group method described below.

The earlier discussion explained that each 1-in-100 public use sample can be subdivided into up to 100 random groups using the subsample number. In general, the variability of the statistic of interest for the sample as a whole is estimated by examining the variability of the statistic among the various random groups within the sample. The random group method is expressed in the following formula:

where q is the statistic of interest computed from the full sample; q _j is the statistic computed from the j^th random group; and t is the number of random groups.

The statistic q may be an index, a regression or correlation coefficient, or other measure for which the following approximate relationship holds:

Eq_j = Eq

where Eq _j and Eqindicate the expected values of the measure for the j^th random group and the full sample respectively. Thus, for example, the formula does not apply for q defined as an estimated total number of persons or housing units in a category.

The procedure specified by the formula for sq² requires the following steps

Use t = 50 when dealing with the 1-in-100 sample or t = 10 with the 1-in-1,000 sample. (See note below for use of other values of t.)
Assign each of the records to one of the t random groups based on the subsample number.
1. To construct 50 random groups, assign all records in which the subsample number is 01 or 51 to the first random group; all records in which the subsample number is 02 or 52 to the second random group; etc. Finally, assign all records in which the subsample number is 50 or 00 random group number 50.
2. To construct 10 random groups of the 1-in-1,000 sample, assign all records with a 1 in the tens digit to random group 1; those with a 2 in the tens digit to random group 2; etc.
Independently within each random group, calculate the desired measure (q _j) as if the records for that random group were the entire sample.
Compute the desired measure (q ) on the entire sample.
Compute the t values (q _j - q )² and apply in the above formula.
The square root of the result is the desired standard error.

Note: The user is cautioned that the standard error given by this procedure is itself subject to sampling error. Some control can be put on the reliability of the estimated s q² by the number of random groups used. The total sample can be separated into different numbers of random groups by different schemes involving the subsample numbers which for the 1-in-100 sample ranges from 00 to 99. Ideally, each random group should represent the total sample.

The number of random groups should be chosen to maximize the reliability of the estimates q². The reliability of the estimated sq ² will depend on the number of degrees of freedom in the estimate (i.e., by the choice of t, the number of random groups), and the number of units in each of the resulting random groups. As a general rule, when estimating sq ² using the 1-in-100 sample, choosing t = 50 would produce reasonably reliable estimates of sq ²for most statistics. One might choose a smaller value for t to estimate the sampling errors for statistics for a given state. The considerations leading to the proper choice of t are described in several statistical texts (for example, Hansen, Hurwitz, Madow, Sample Survey Methods and Theory,Vol. I, Chapter 10, Section 16, page 440 ff).

For the 1-in-1,000 sample, the tens digits of the subsample number ranges from 0 to 9 and can be used to define 10 random groups (the units digit is fixed). When this sample is being used, the choice of t is limited to a maximum of t = 10.

ENDNOTES:

Originally published as "Chapter IV, Guidelines for Use of the Samples;" and Chapter V, "Sample Design and Computation of Standard Errors;" Public Use Samples of Basic Records from the 1970 Census: Description and Technical Documentation, U.S. Department of Commerce, Bureau of the Census, April 1972, pp. 179-191 and 194-203.
The exact formula for the applicable factor is: 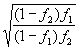where f1 = 1,100 and f2 - 1/1000. For sample sizes this small the factor 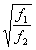is an adequate approximation.

Go Back to Sampling Procedures Index

1970 Sampling Variability, Sampling Design and Computation of Standard Errors1